M3D-C1 Overview
[
M3D-C1 Home |
M3D-C1 Overview |
M3D-C1 Users Guide(old) |
M3D-C1 Users Guide(new-in progress) |
Weekly Meeting Minutes |
User License Agreement |
M3DC1 Publications
]
M3D-C1 is a code that solves the extended-magnetohydrodynamic
(MHD) equations, which is a model that describes plasma as
electrically conducting fluids of ions and electrons. This
code is primarily used for calculating the equilibrium,
stability, and dynamics of fusion plasmas, but has also been
used for a variety of
other applications,
including astrophysical applications. In particular, M3D-C1
is designed to address some of the most critical challenges
confronting tokamak plasmas: large-scale instabilities, which
significantly degrade thermal confinement; and disruptions,
which cause complete loss of energy confinement and which may
cause damage to reactor-scale tokamaks such as ITER.
M3D-C1 builds upon some of the design principles pioneered by
M3D, but the
two codes are developed independently and do not share source
code. The "C1" in M3D-C1 refers to the $C^1$ property of its
finite elements, which ensures that both the value and the
derivatives of fields are continuous across mesh element
boundaries.
Advanced numerical
methods are employed in M3D-C1 to permit the efficient
solution of its numerical model over a broad range of
temporal and spatial scales. These methods include the use
of high-order finite elements on an unstructured mesh; fully
implicit and semi-implicit time integration options;
physics-based preconditioning; and parallelization via
domain decomposition and the use of scalable parallel sparse
linear algebra solvers.
Documents describing how to use and run the code, and
publications describing the numerical methods and physics
results in more detail, can be found in
the reference
documents and
the bibliography below.
Vertical Displacement Events (VDEs)
|
Vertical Displacement Events (VDEs) are disruptions that
occur when the vertical control of a tokamak plasma is
lost, and the plasma rapidly moves upward or downward
into the inner walls of the confinement vessel. These
events not only terminate the plasma discharge, but may
cause enormous heat loads and electromagnetic stresses
on the vessel.
M3D-C1 is being used to characterize these
instabilities, to gain insight into the location and
magnitude of the expected heat loads and thermal
stresses. The resistive wall model in M3D-C1 allows the
modeling of "Halo currents," which are electrical
currents that flow from the plasma to the wall and back.
These currents are thought to be responsible for a
significant fraction of the electromagnetic forces on
the vessel during a disruption.
|
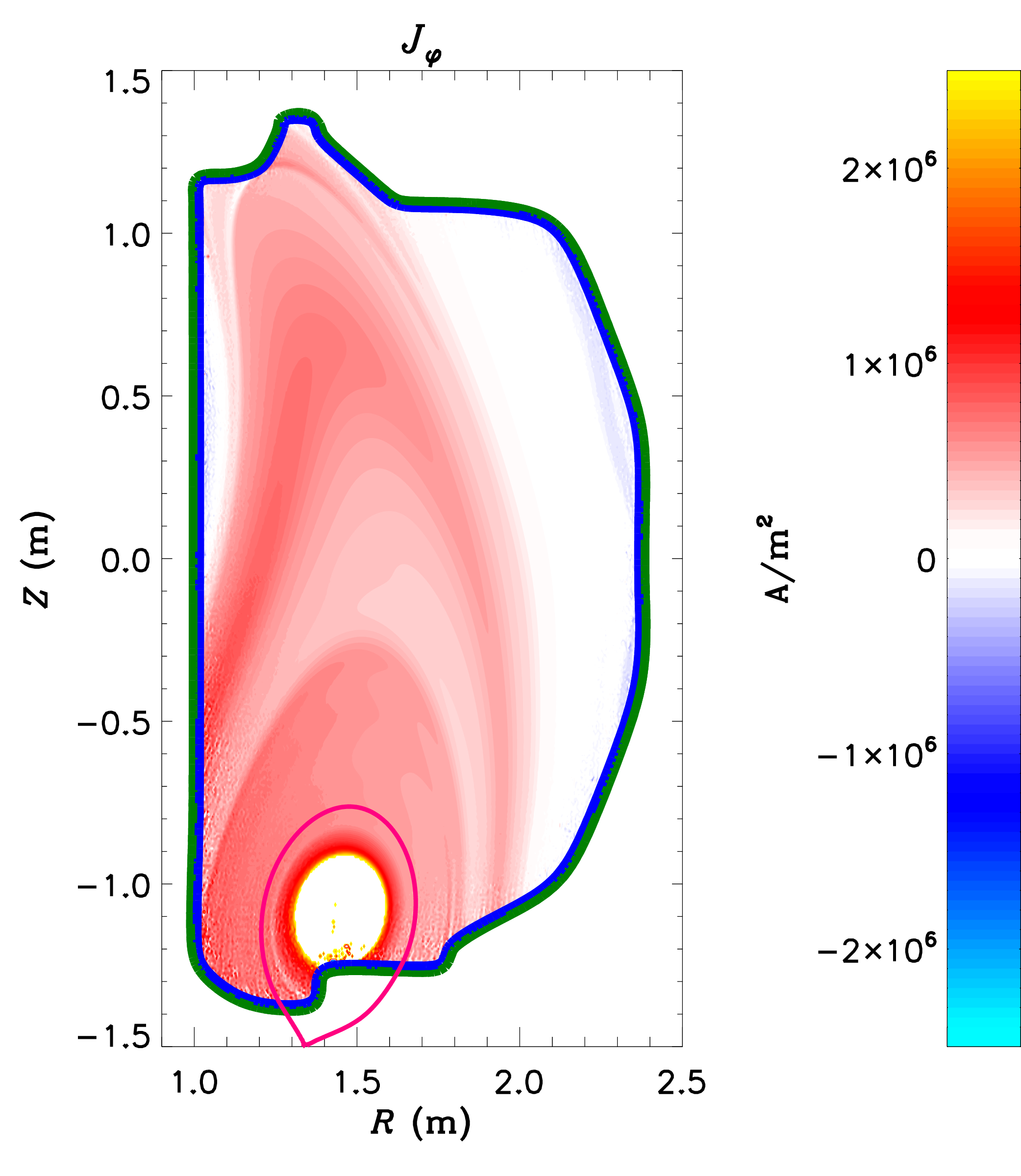
|
A description of 2D VDE calculations with M3D-C1 is given
in NM
Ferraro, et al. Phys. Plasmas 23:056114
(2016).
Sawteeth and Helical Core Equilibria
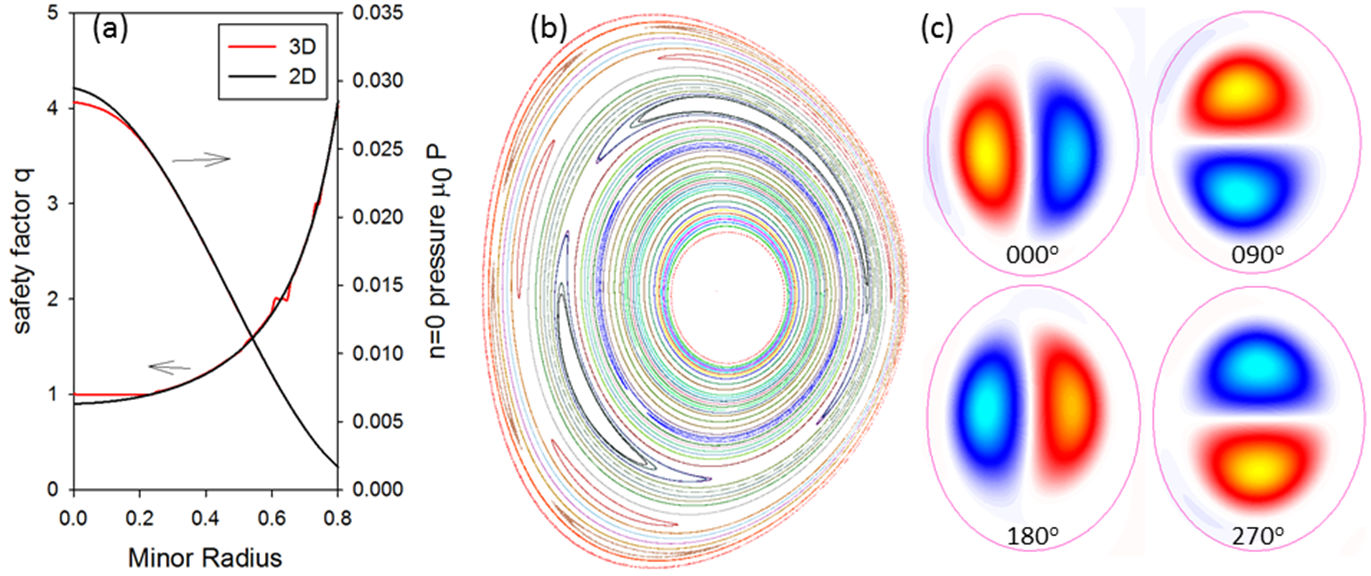 (a) $q$-profile and toroidally-averaged $p$ for 3D run, and 2D
run with the same transport coefficients.
(a) $q$-profile and toroidally-averaged $p$ for 3D run, and 2D
run with the same transport coefficients.
(b) Poincare
plot in the final state with $(2, 1)$ and $(3, 1)$ islands
present (central volume has $q=1$).
(c) Contours of
electrostatic potential, $\phi$, produced by the stationary
interchange mode.
In most tokamak discharges, the plasma current slowly peaks
until it becomes unstable to internal kink modes. This
so-called "sawtooth" instability flattens the central current;
at which time the process repeats. While these oscillations
are generally benign, they are likely best avoided in burning
plasmas: high-energy fusion products ($\alpha$-particles) can
increase the oscillation amplitude, which may excite
neoclassical tearing modes and/or edge localized modes,
potentially causing major disruptions. Using the M3D-C1 code
another mechanism for preventing the current from peaking that
involves a self-organized, dynamo action was found,
which avoids these problems.
Numerical simulations and analytic theory have determined
that, for certain, global parameters, the plasma will
self-organize with the central safety-factor, $q$, slightly
above unity and constant in a central volume (as shown in
above figure, click to enlarge), where $q$ is defined as how
many times a magnetic field line travels around the torus the
long way compared to the short way.
Such a large, "shear"-free region is unstable to
pressure-driven "interchange" modes.
The linearly-unstable, interchange eigenfunction extends
throughout the shear-free region and drives a strong,
stationary, $(1,1)$-helical flow that then drives a stationary
$(1,1)$-component of the electrostatic potential, $\phi$,
(shown) and of the magnetic field (shown).
These combine to create a $(0,0)$-"dynamo" voltage
that prevents the current density from peaking in the
center, hence maintaining the shear-free region with $q$
slightly above unity in the central region, and with a broad
current profile.
This mechanism could explain the physics behind the
non-sawtoothing "hybrid" discharges observed in DIII-D and in
many other tokamaks.
For more details,
see
SC Jardin, N Ferraro, I
Krebs. Phys. Rev. Lett. 115:215001 (2015).
Edge-Localized Modes (ELMs)
The high-confinement mode (H-mode) of tokamak plasma operation
is characterized by steep thermal gradients and large current
densities at the edge of the plasma. While H-mode is
advantageous from a confinement standpoint, the large pressure
gradients and current densities lead to periodic instabilities
known as Edge Localized Modes (ELMs) that intermittently
deliver significant heat loads to plasma-facing components of
the confinement vessel. In reactor-scale devices like ITER,
these heat loads may be large enough to rapidly erode these
components, and therefore must be mitigated.
M3D-C1 has been used to calculate how various non-ideal
effects, including resistivity, rotation, and two-fluid terms
change ELM stability. For example,
see NM Ferraro
(2010). M3D-C1 has also been used to simulate the
nonlinear evolution of ELMs, in order to better understand the
thermal transport that these modes cause.
Linear Response to Applied 3D Fields
|
The magnetic fields in tokamaks are nominally axisymmetric
(independent of toroidal angle). It has been observed,
however, that applying small non-axisymmetric fields to the
plasma can have a significant effect on confinement and ELM
stability. In particular, ELM suppression through the
application of non-axisymmetric fields is one of the primary
techniques for mitigating the intermittent heat bursts caused
by ELMs.
It is not yet understood why applying non-axisymmetric fields
sometimes mitigates or suppresses ELMs. Part of the
difficulty in understanding this process is that the applied
field drives currents in the plasma, which themselves create
non-axisymmetric fields. These "plasma response" fields are
often stronger than the applied fields themselves. So a
challenge in understanding these effects is being able to
calculate the plasma response given the applied fields.
Developing this understanding is crucial for being able to
confidently design coils for this technique on reactor-scale
devices.
M3D-C1 has been used extensively to calculate the plasma
response to applied fields in DIII-D, AUG, NSTX, NSTX-U,
KSTAR, and model ITER plasmas.
|
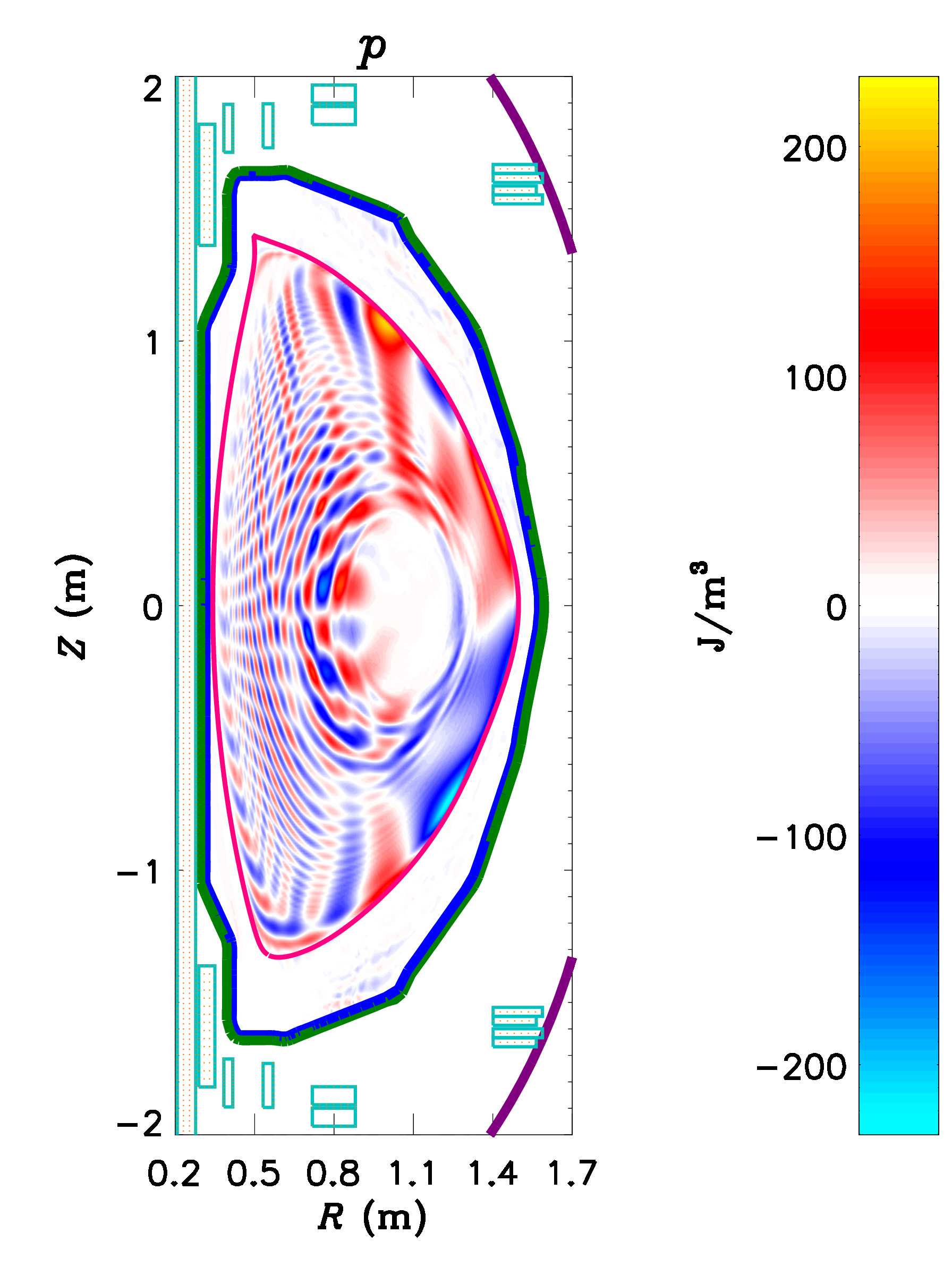 The
pressure perturbations that will be produced by applying
non-axisymmetric fields from the proposed Non-axisymmetric
Control Coils (NCC) to a model NSTX-U equilibrium, as
calculated by M3D-C1. The
pressure perturbations that will be produced by applying
non-axisymmetric fields from the proposed Non-axisymmetric
Control Coils (NCC) to a model NSTX-U equilibrium, as
calculated by M3D-C1.
|
The extended-MHD model implemented in M3D-C1 consists of a set
of fluid equations which evolve the particle number density
$n$, fluid velocity $\vec{u}$, total pressure $p$, and
electron pressure $p_e$:
\begin{eqnarray}
\frac{\partial n}{\partial t} + \nabla \cdot (n \vec{u}) & = & 0
\\
n m_i \left(\frac{\partial \vec{u}}{\partial t} + \vec{u} \cdot
\nabla \vec{u} \right)
& = & \vec{J} \times \vec{B} - \nabla p
\color{blue}{ \mbox{} - \nabla \cdot \Pi + \vec{F}}
\\
\frac{\partial p}{\partial t} + \vec{u} \cdot \nabla p + \Gamma p
\nabla \cdot \vec{u} & = &
\color{blue}{(\Gamma - 1) \left[Q - \nabla \cdot \vec{q} +
\eta J^2 - \vec{u} \cdot \vec{F} - \Pi : \nabla u \right]}
\\ & & \color{red}{\mbox{} +
\frac{1}{n e} \vec{J} \cdot \left( \frac{\nabla
n}{n} p_e - \nabla p_e \right)
+ (\Gamma-1) \Pi_e : \nabla \left(\frac{1}{n e} \vec{J} \right)}
\\
\frac{\partial p_e}{\partial t} + \vec{u} \cdot \nabla p_e
+ \Gamma p_e
\nabla \cdot \vec{u} &
= &
\color{blue}{(\Gamma - 1) \left[Q_e - \vec{q}_e + \eta J^2
- \vec{u} \cdot \vec{F}_e - \Pi_e : \nabla u \right]}
\\ & &
\color{red}{\mbox{} + \frac{1}{n e} \vec{J} \cdot \left( \frac{\nabla
n}{n} p_e - \nabla p_e \right) +
(\Gamma-1) \left[
\Pi_e : \nabla \left(\frac{1}{n e} \vec{J} \right)
+ \frac{1}{n e} \vec{J} \cdot \vec{F}_e \right]}
\end{eqnarray}
a generalized Ohm's law, in which the electric field $\vec{E}$
is obtained from the equations describing conservation of
electron momentum and charge:
\begin{equation}
\vec{E} = - \vec{u} \times \vec{B}
\color{blue}{ \mbox{} +\eta \vec{J}}
\color{red}{ \mbox{} +
\frac{1}{n e} \left( \vec{J} \times \vec{B} - \nabla p_e
- \nabla \cdot \Pi_e + \vec{F}_e \right)}
\end{equation}
and a reduced set of Maxwell's equations which relates the
electrical current density $\vec{J}$ in the plasma to the
magnetic field $\vec{B}$ and describes the evolution of the
magnetic field:
\begin{eqnarray}
\vec{J} & = & \frac{1}{\mu_0} \nabla \times \vec{B}
\\
\frac{\partial \vec{B}}{\partial t} & = & -\nabla \times \vec{E}
\end{eqnarray}
The "Ideal-MHD" model is a subset of the one described above,
which is obtained in the limit where external sources,
dissipative terms (like viscosity and resistivity) and the ion
Larmor radius are zero, leaving only the terms colored
black. "Single-Fluid MHD" is a
larger subset, in which the ions and electrons are considered
to have the same fluid velocity and temperature, but where
dissipative terms and external sources are included, shown in
blue. M3D-C1 implements a
"Two-Fluid" model, which takes
differences in the ion and electron fluid velocities into
account, which introduces the terms colored red. M3D-C1 may
also be used for solving the single-fluid equations. The
ideal-MHD equations are best solved using specialized codes
such as DCON, IPEC, GATO, ELITE, VMEC, or SPEC, which are
designed to take advantage of special properties of the
ideal-MHD equations.
$\vec{F} = \vec{F}_i + \vec{F}_e$, where $\vec{F}_i$ and
$\vec{F}_e$ are external forces acting on the ions and
electrons, respectively (e.g. gravity). Similarly, $Q
= Q_i + Q_e$, where $Q_i$ and $Q_e$ are external sources of
heat to the ions and electrons. In M3D-C1, several processes
are implemented that are represented by these sources,
including neutral beam injection.
The viscous stress tensor $\Pi = \Pi_i + \Pi_e$ is the sum of
the ion and electron stress tensors. Several processes
contributing to the ion stress tensor are implemented:
\begin{equation}
\Pi_i = \Pi_i^\perp + \Pi_i^\wedge + \Pi_i^\parallel
\end{equation}
where $\Pi_i^\perp$ is the perpendicular ion viscosity, which
represents simple cross-field angular momentum diffusivity;
$\Pi_i^\wedge$ is the ion gyroviscosity, which represents
finite ion Larmor radius effects; and $\Pi_i^\parallel$
is the parallel ion viscosity, which represents pressure
anisotropy and is responsible for ion sound wave damping and
poloidal flow damping in the extended-MHD model. Presently,
the $\Pi_e$ term is implemented as a hyper-resistive term.
The heat flux density $\vec{q} = \vec{q}_i + \vec{q}_e$ is the
sum of the ion and electron heat flux densities, which
themselves are represented as the sum of perpendicular and
parallel parts:
\begin{equation}
\vec{q}_{(i,e)} = -\kappa_{(i,e)}^\perp \nabla T_{(i,e)} -
\kappa_{(i,e)}^\parallel \frac{\vec{B} \vec{B} \cdot \nabla T_{(i,e)}}{B^2}
\end{equation}
M3D-C1's equations are formulated in $(R,\varphi,Z)$
coordinates, and do not make use of magnetic coordinates.
Therefore there is no coordinate singularity at poloidal field
nulls (such as the magnetic axis or x-points of toroidal
plasmas), and no need to impose boundary conditions there.
The model implemented in M3D-C1 contains far more options than
can be reasonably described here. For a more detailed,
complete, and up-to-date description of the model implemented
in M3D-C1, please refer to
the
M3D-C1 Model Reference.
Reduced Models
A useful feature of M3D-C1 is that it represents the magnetic
field and fluid velocity using stream functions and potentials,
similar to a Helmholtz decomposition:
\begin{eqnarray}
\vec{B} & = & \nabla \psi \times \nabla \varphi + F \nabla
\varphi
\\
\vec{u} & = & R^2 \nabla U \times \nabla \varphi + R^2 \omega
\nabla \varphi + R^{-2} \nabla_\perp \chi
\end{eqnarray}
One advantage of this representation is that the magnetic
field is manifestly divergence-free. Another advantage is
that we obtain physically meaningful reduced models by
restricting the set of scalar fields that are evolved.
Specifically, we obtain the two-field reduced model by only
considering the evolution of $\psi$ and $U$, and we obtain the
four-field reduced model by only considering the evolution of
$\psi$, $U$, $F$, and $\omega$. These reduced models provide
accurate solutions in certain physical limits, at a fraction
of the computational cost of the full extended-MHD model.
Resistive Wall
M3D-C1 optionally includes a resistive wall model, which is
treated as a spatially resolved region of arbitrary thickness.
This capability enables the study of so-called "resistive wall
modes" (RWMs) in tokamaks, which are external kink modes that
would be stable in the presence of a perfectly conducting
wall, but which are unstable when the wall has finite
resistivity.
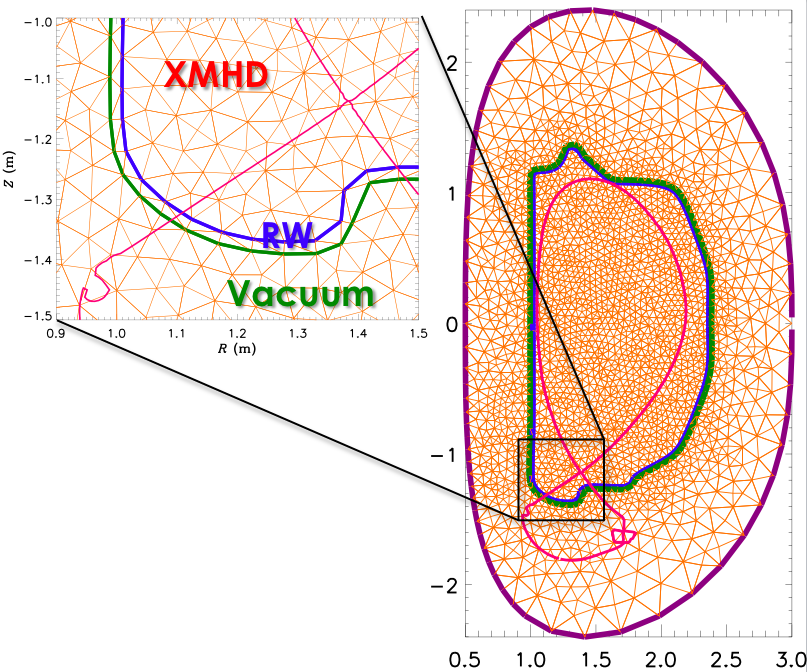
|
In calculations that include a resistive wall, the
computational domain is divided into three parts. The
innermost part is the extended-MHD (XMHD)
region, in which the full extended-MHD model is solved.
Enclosing this region is the resistive wall
(RW) region, in which only Maxwell's equations are
solved, with $\vec{E} = \eta_w \vec{J}$. Enclosing this
region is the vacuum region, where only
$\eta{J} = 0$ is solved. The equations in these regions
are solved self-consistently and simultaneously, using
implicit time-stepping methods.
|
More information about the implementation and application of the
resistive wall capability in M3D-C1 can be found
in NM
Ferraro, et al. Phys. Plasmas 23:056114
(2016).
Finite Elements
In its 2D and 2D-complex modes of operation, M3D-C1 uses
two-dimensional, reduced-quintic triangular finite elements on
an unstructured mesh. These high-order, $C^1$ elements are
described in detail
in SC
Jardin J. Comp. Phys. 200:133 (2004).
In its 3D mode of operation, M3D-C1 uses three-dimensional
triangular-prism elements that are a tensor product of the
triangular reduced-quintic elements in the poloidal plane with
cubic Hermite elements in the toroidal (or axial) direction.
These three-dimensional elements also have the $C^1$ property.
Implicit and Semi-Implicit Time Advance
-
User's Guide: Comprehensive reference that
covers building and running M3D-C1, mesh generation, example
problems, and descriptions of the input files.
-
Model Reference: A description of the physics model
implemented in M3D-C1 and the input parameters controlling
the model.
-
Tutorial: A short reference guide describing
running the code for some common use cases.
-
IDL Reference: A description of the IDL visualization and
post-processing routines provided with M3D-C1
-
Release Notes: A list of new features in each release of
M3D-C1
-
Normalization Spreadsheet: A spreadsheet for translating
between M3D-C1 normalized units and physical units
To run or obtain the source code for M3D-C1 please complete
and submit the PPPL Theory
Codes
License-Release form. Please note that this agreement
requires that a designee of PPPL be allowed to review any
output of M3D-C1 prior to publication to help ensure that the
code has been run correctly and that the results have been
properly interpreted.
The development of M3D-C1 has been supported by the US
Department of Energy through
the Center for Extended MHD
Modeling (CEMM)
and Center
for Tokamak Transient Simulations
(CTTS) SciDAC activities.
The numerical tools and methods relating to meshing and domain
decomposition are developed through a collaboration with
the RPI SCOREC group.
The following is a list of publications that focus primarily
on M3D-C1 modeling or numerical methods. It does not include
publications that feature M3D-C1 calculations in support of
understanding specific experiments.
If you would like to cite M3D-C1, please see the list
of references by
subject to find the best appropriate references.
-
BC Lyons, CC Kim, YQ Liu, NM Ferraro, SC Jardin, J
McClenaghan, PB Parks, LL Lao.
"Axisymmetric benchmarks of impurity dynamics in
extended-magnetohydrodynamic simulations."
Plasma Phys. Control. Fusion 61:064001 (2019)
-
NM Ferraro, BC Lyons, CC Kim, YQ Liu, and SC Jardin.
"3D two-temperature magnetohydrodynamic modeling of fast
thermal quenches due to injected impurities in tokamaks."
Nucl. Fusion 59:016001 (2019)
-
D Pfefferle, N Ferraro, SC Jardin, I Krebs, and A
Bhattacharjee. "Modelling of NSTX hot vertical
displacement events using M3D-C1."
Phys. Plasmas 25:056106 (2018)
-
NM Ferraro, SC Jardin, LL Lao, MS Shephard, F Zhang.
"Multi-region approach to free-boundary three-dimensional
tokamak equilibria and resistive wall instabilities."
Phys. Plasmas 23:056114 (2016)
-
F Zhang, R Hager, S-H Ku, C-S Chang,
SC Jardin, NM Ferraro, S Seol,
E Yoon, MS Shephard.
"Mesh generation for confined fusion plasma simulation."
Engineering with Computers p. 1–9 (2015)
-
NM Ferraro.
"Calculations of two-fluid linear response to
non-axisymmetric fields in tokamaks."
Phys. Plasmas 19:056105 (2012)
-
SC Jardin, N Ferraro, J Breslau, J Chen.
"Multiple timescale calculations of sawteeth and other
global macroscopic dynamics of tokamak plasmas."
Comp. Sci. & Disc. 5:014002 (2012)
-
NM Ferraro, SC Jardin, PB Snyder.
"Ideal and resistive edge stability calculations with
M3D-C1."
Phys. Plasmas 17:102508 (2010)
-
NM Ferraro, SC Jardin.
"Calculations of two-fluid magnetohydrodynamic
axisymmetric steady-states."
J. Comp. Phys. 228:7742 (2009)
-
J Breslau, N Ferraro, S Jardin.
"Some properties of the M3D-C1 form of the
three-dimensional magnetohydrodynamics equations."
Phys. Plasmas 16:092503 (2009)
-
SC Jardin, N Ferraro, X Luo, J Chen, J Breslau, KE Jansen,
MS Shephard.
"The M3D-C1 approach to simulating 3D 2-fluid
magnetohydrodynamics in magnetic fusion experiments."
J. Phys.: Conf. Series 125:012044 (2008)
-
SC Jardin, J Breslau, N Ferraro.
"A high-order implicit finite element method for
integrating the two-fluid magnetohydrodynamic equations in
two dimensions."
J. Comp. Phys. 226:2146 (2007)
-
NM Ferraro and SC Jardin. "Finite element implementation
of Braginskii's gyroviscous stress with
application to the gravitational instability."
Phys. Plasmas 13:092101 (2006)
-
SC Jardin. "A triangular finite element with
first-derivative continuity applied to fusion MHD
applications." J. Comp. Phys. 200:133
(2004)
References By Subject
The following list includes some of the best references for
the implementation of various models in M3D-C1, as well as some
references to the application of the code to physical
phenomena.
- Disruption Mitigation:
Ferraro 2019,
Lyons 2019,
Fil 2017
- Edge Localized Modes
Ferraro 2010,
Wingen 2015
- Impurity Model:
Ferraro 2019
- MHD Model:
Breslau 2009
- Non-axisymmetric Tokamak Equilibria (nonlinear):
Jardin 2015,
Krebs 2017,
Reiman 2015
- Pellet Model:
Lyons 2019
- Perturbed Tokamak Equilibria (linear):
Ferraro 2012,
Ferraro 2013,
Lyons 2017,
Canal 2017,
Wingen 2015,
Reiman 2015
- Resistive Wall Model:
Ferraro 2016
- Resistive Wall Modes:
Ferraro 2016
- Sawteeth:
Jardin 2015,
Jardin 2012
- Vertical Displacement Events:
Pferrerle 2018,
Ferraro 2016

 (a) $q$-profile and toroidally-averaged $p$ for 3D run, and 2D
run with the same transport coefficients.
(a) $q$-profile and toroidally-averaged $p$ for 3D run, and 2D
run with the same transport coefficients. The
pressure perturbations that will be produced by applying
non-axisymmetric fields from the proposed Non-axisymmetric
Control Coils (NCC) to a model NSTX-U equilibrium, as
calculated by M3D-C1.
The
pressure perturbations that will be produced by applying
non-axisymmetric fields from the proposed Non-axisymmetric
Control Coils (NCC) to a model NSTX-U equilibrium, as
calculated by M3D-C1.
